数据结构与算法之美学习笔记

基础篇之数组

在大部分编程语言中，数组都是从0开始编号的，你知道为什么数组要从0开始编号，而不是从1开始编号呢？从1开始不是更符合人类的思维习惯吗？

什么是数组

数组(Array)是一种线性表数据结构。它用一组连续的内存空间，来存储一组具有相同类型的数据。

几个关键词

1. 线性表(Linear List)。

   线性表就是数据排成像一条线一样的结构。每个线性表上的数据最多只有前和后两个方向。除了数组，链表、队列、栈等也是线性表结构。

   

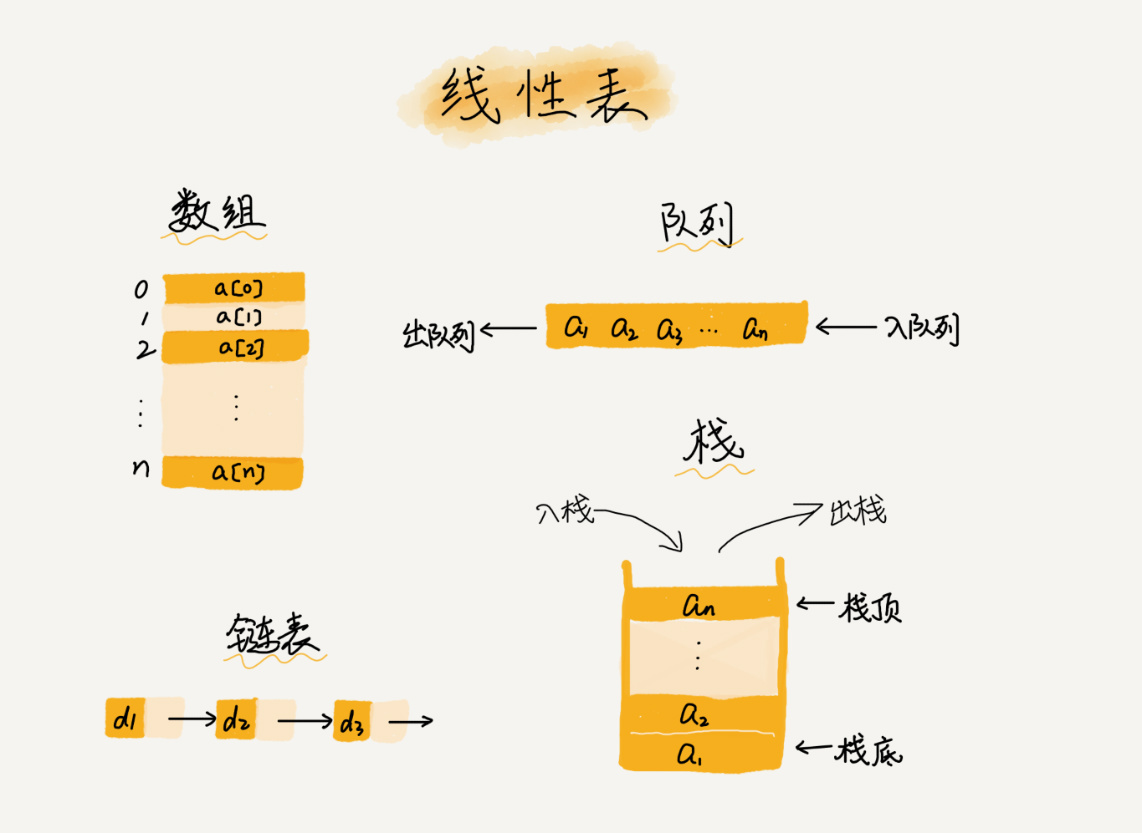
   与之相对的是非线性表，如二叉树、堆、图等。因为在非线性表中，数据之间并不是简单的前后关系。

   

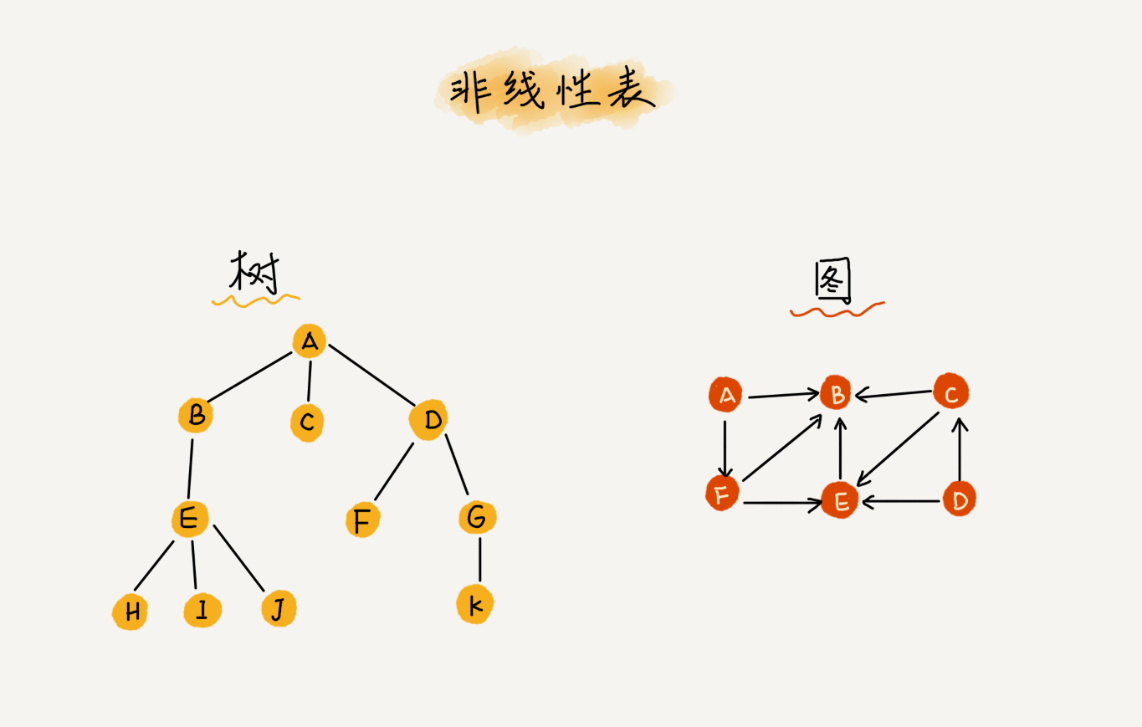
2. 连续的内存空间和相同类型的数据。

   因为这两个限制，数组有个优势：随机访问。也有个劣势：数组的很多操作变得非常低效。例如在数组中删除、插入一个数据，为了保证连续性，需要做大量的数据搬移工作。

数组是如何实现根据下标随机访问数组元素的

举个例子，数组 int[] a = new int[10]，如下图，计算机给数组a[10]分配了一块连续内存空间1000-1039，其内存块的首地址为base_address = 1000。

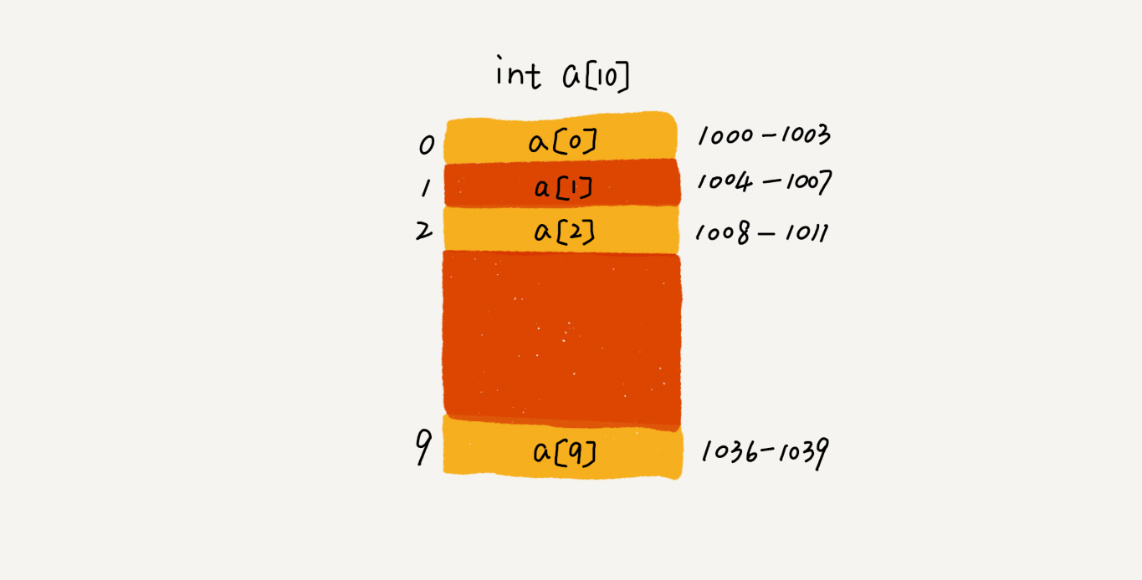
计算机会给每个内存单元分配一个地址，计算机通过地址来访问内存中的数据。计算机随机访问数组中的某个元素时，根据以下公式来进行寻址：

a[i]_address = base_address + i * data_type_size

data_type_size:表示数组中每个元素的大小。这里是int类型，所以data_type_size为4个字节。

数组和链表的区别

非准确表述：链表适合插入、删除，时间复杂度 O(1)；数组适合查找，查找时间复杂度为 O(1)¹

准确表述：链表适合插入、删除，时间复杂度 O(1)；数组支持随机访问，根据下标随机访问的时间复杂度为O(1)。

低效的“插入”和“删除”

插入操作

假设数组长度为n，如果把一个数据插入到数组中的第K个位置，那插入操作的时间复杂度是多少呢？

如果在数组末尾插入元素，不用移动数据，时间复杂度为O(1)，如果在数组元素开头插入元素，所有数组元素都需要依次往后移动一位，则最坏时间复杂度为O(n)。因为在每个位置插入元素的概率是一样的，所以平均情况时间复杂度为(1+2+…+n)/n = O(n)。

插入优化

如果数组中存储的数据没有任何规律，数组只是被当作一个存储数据的集合，如果将某个数据插入到第K个位置，则可以将第K位的数据搬移到数组元素的最后，把新元素直接放入到第K个位置。

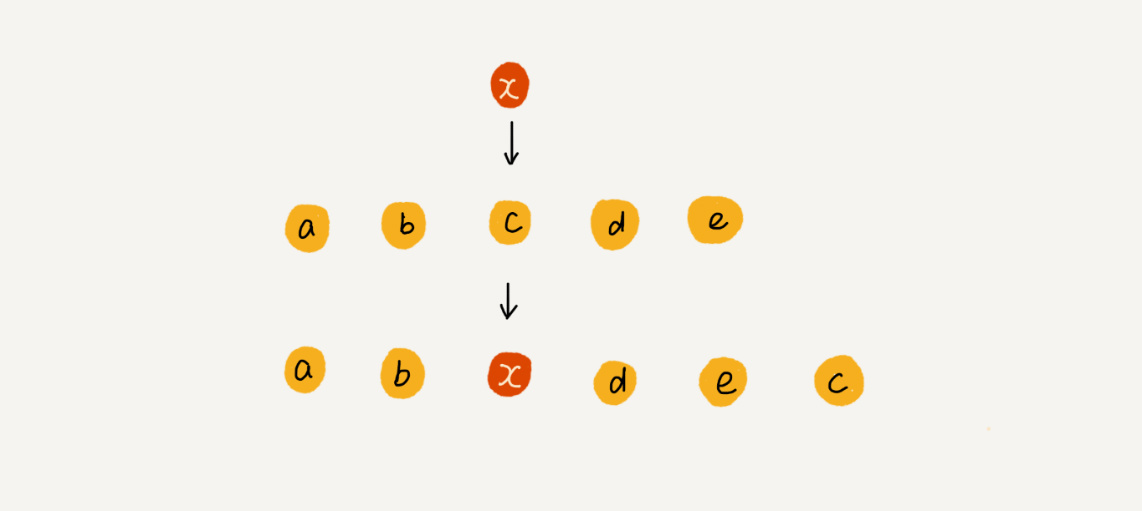
这样在特定场景下，在第K个位置插入元素的时间复杂度就降为O(1)。快排也会用到这个思想。

删除操作

如果要删除第K个位置的数据，为了内存的连续性，也需要搬移数据，不然中间出现空洞，内存不再连续。

和插入类似，如果删除数组末尾的数据，则最好情况时间复杂度为O(1)，如果删除开头的数据，则最坏情况时间复杂度为O(n)；平均情况时间复杂度也为O(n)。

删除优化

数组a[10]中存储了8个元素：a,b,c,d,e,f,g,h。现在我们要依次删除a，b，c三个元素

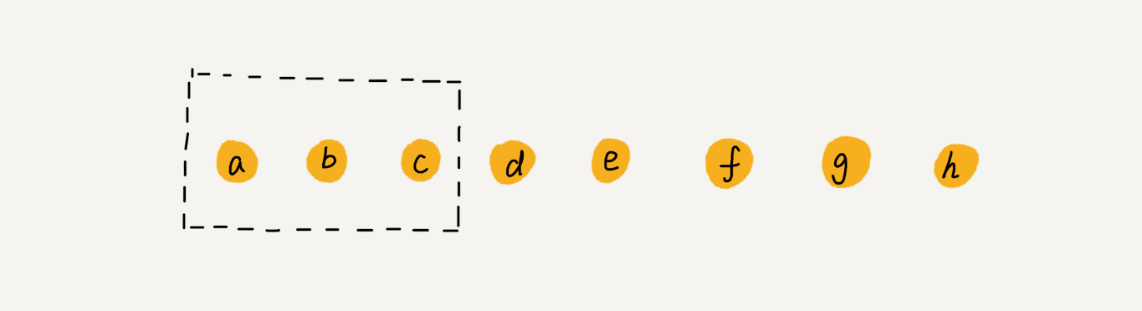
为了避免d，e，f，g，h这几个数据会被搬移三次，我们可以先记录已经删除的数据。每次的删除操作并不是真正地搬移数据，只是记录数据已经被删除。当数组没有更多空间存储数据时，我们再触发执行一次真正地删除操作，这样就大大减少了删除操作导致的数据搬移。

如果你了解JVM，你会发现这就是JVM标记清除垃圾回收算法的核心思想。

很多时候我们并不是要去死记硬背某个数据结构或者算法，而是要学习它背后的思想和处理技巧，这些东西才是最有价值的

警惕数组的访问越界问题

分析这段C代码的运行结果：

int main(int argc, char* argv[]){
    int i = 0;
    int arr[3] = {0};
    for(; i<=3; i++){
        arr[i] = 0;
        printf("hello world\n");
    }
    return 0;
}

这段代码运行结果并非打印三行“hello world”，而是会无限打印，why？²

因为数组大小为3，a[0]，a[1]，a[2]，由于我们编码错误，导致for循环的结束条件错写为了i<=3 而非 i<3，所以当i=3时，数组a[3]访问越界。

在C语言中，只要不是访问受限的内存，所有的内存空间都是可以自由访问的。根据数组寻址公式，a[3]会被定位到某块不属于数组的内存地址上，而这个地址正好是存储变量i的内存地址，那么a[3]=0 就相当于 i=0，所以就会导致代码无限循环。

数组越界在 C 语言中是一种未决行为，并没有规定数组访问越界时编译器应该如何处理。因为，访问数组的本质就是访问一段连续内存，只要数组通过偏移计算得到的内存地址是可用的，那么程序就可能不会报任何错误。

但并非所有的语言都像C一样，把数组越界检查的工作丢给程序员来做，Java就会做越界检查，上面的代码在Java中会抛出java.lang.ArrayIndexOutOfBoundsException。

容器能否完全替代数组

容器类ArrayList(Java)的优势：可以将很多数组操作的细节封装起来，比如数组插入、是删除数据时的数据搬移。另一个优势是支持动态扩容(自动扩容1.5倍)。

由于扩容操作涉及到内存申请和数据搬移，是比较耗时的。如果事先能确定要存储的数据大小，最好在创建ArrayList的时候事先指定数据大小。比如List list = new ArrayList(1000)

适用于数组替代容器类的情况：

1. Java ArrayList无法存储基本类型，比如int、long，需要封装为Integer、Long类，而Autoboxing、Unboxing是有一定的性能消耗。若果特别关注性能，或者希望使用基本类型，可以选用数组。
2. 如果数据大小事先已知，并且对数据的操作非常简单，用不到ArrayList提供的大部分方法，也可以直接使用数组。
3. 当要表示多维数组时，用数组会更加直观。比如Object[][] arr，如果容器类要这样定义则：ArrayList<ArrayList> arr。

总结：对于普通的业务开发，使用容器类就足够了，省时省力，性能损耗一丢丢，不会影响到系统整体的性能。如果做一些非常底层的开发，比如网络架构，性能的优化需要做到极致，这个时候数组优于容器类，成为首选。

解答开篇

为什么大多数编程语言中，数组要从0开始编号，而不是从1开始编号？

从数组存储的内存模型上来看，“下标”最确切的定义应该是“偏移（offset）”。前面也讲到，如果用 a 来表示数组的首地址，a[0] 就是偏移为 0 的位置，也就是首地址，a[k] 就表示偏移 k 个 type_size 的位置，所以计算 a[k] 的内存地址只需要用这个公式：

a[k]_address = base_address + k * type_size

但是，如果数组从 1 开始计数，那我们计算数组元素 a[k] 的内存地址就会变为：

a[k]_address = base_address + (k-1)*type_size

对比两个公式，我们不难发现，从 1 开始编号，每次随机访问数组元素都多了一次减法运算，对于 CPU 来说，就是多了一次减法指令。

数组作为非常基础的数据结构，通过下标随机访问数组元素又是其非常基础的编程操作，效率的优化就要尽可能做到极致。所以为了减少一次减法操作，数组选择了从 0 开始编号，而不是从 1 开始。

上面解释其实都算不上压倒性的证明，说数组起始编号非 0 开始不可。所以我觉得最主要的原因可能是历史原因。

C 语言设计者用 0 开始计数数组下标，之后的 Java、JavaScript 等高级语言都效仿了 C 语言，或者说，为了在一定程度上减少 C 语言程序员学习 Java 的学习成本，因此继续沿用了从 0 开始计数的习惯。实际上，很多语言中数组也并不是从 0 开始计数的，比如 Matlab。甚至还有一些语言支持负数下标，比如 Python。

小结

数组用一块连续的内存空间，来存储相同类型的一组数据，最大的特点就是支持随机访问，但插入、删除操作也因此变得比较低效，平均情况时间复杂度为 O(n)。在平时的业务开发中，我们可以直接使用编程语言提供的容器类，但是，如果是特别底层的开发，直接使用数组可能会更合适。

思考

1. 你理解的JVM标记清除垃圾回收算法³。
2. 二维数组的寻址公式⁴。

• Previous
  数据结构与算法之美学习笔记
• Next
  数据结构与算法之美学习笔记