数据结构与算法之美学习笔记

基础篇之排序(下)

你知道如何在O(n)的时间复杂度内查找一个无序数组中的第K大元素吗？

归并排序的原理

如果要排序一个数组，我们先把数组从中间分成前后两部分，然后对前后两部分分别排序，再将排好序的两部分合并在一起，这样整个数组就都有序了。

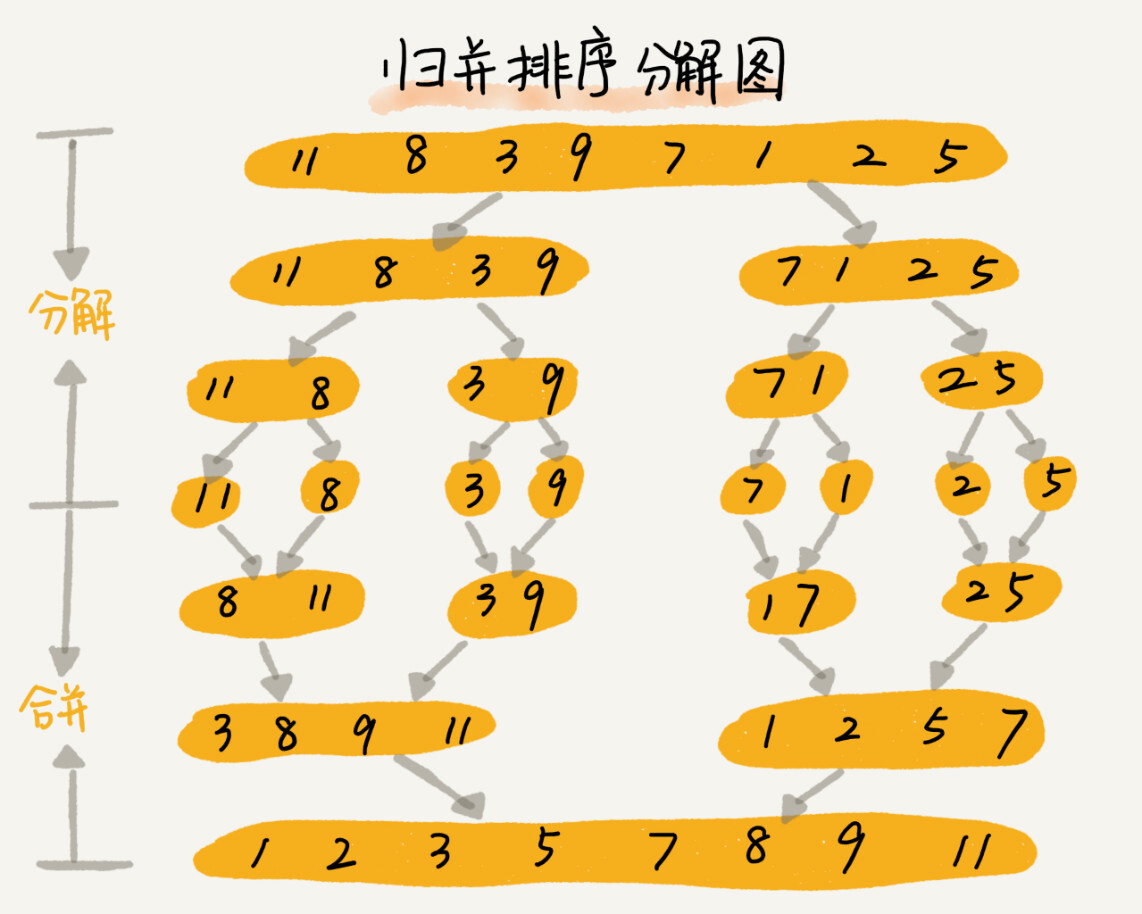
归并排序使用的就是分治思想。分治，就是分而治之，将一个大问题分解成小的子问题来解决。小的问题解决了，大问题也就解决了。

分治思想和递归思想很像。分治算法一般都是用递归来实现的。分治是一种解决问题的处理思想，递归是一种编程技巧，这两者并不冲突。

如何用递归代码来实现归并排序？

递归代码的编程技巧是，分析得出递推公式，然后找到终止条件，最后将递推公式翻译成递归代码。所以，想要写出归并排序的代码，我们先写出归并排序的递推公式。

//递推公式
merge_sort(p...r) = merge(merge_sort(p...q), merge_sort(q+1...r))
//终止条件
p >= r 不用再继续分解

其中，merge_sort(p…r)表示，给下标从p到r之间的数组排序。我们将这个排序问题转化为了两个子问题，merge_sort(p…q)和merge_sort(q+1…r)，其中下标q等于p和r的中间位置，也就是(p+r)/2。当下标从p到q和从q+1到r这两个子数组都排好序之后，我们再将两个有序的子数组合并在一起，这样下标从p到r之间的数据就也排好序了。

根据这个递推公式和终止条件，得出下面的代码

//归并排序算法， a 是数组，n 表示数组大小
public void mergeSort(int[] a, int n) {
  mergeSortC(a, 0, n-1);
}
//递归调用函数
public void mergeSortC(int[] a, int p, int r) {
  //递归终止条件
  if (p >= r) return;
  
  //取 p 到 r 之间的中间位置q
  int q = (p + r) / 2;
  //分治递归
  mergeSortC(a, p, q);
  mergeSortC(a, q+1, r);
  //将a[p...q] 和 a[q+1...r] 合并为 a[p...r]
  merge(a, p, r, q); //merge(a[p...r], a[p...q], a[q+1...r]);
}

merge(a[p…r], a[p…q], a[q+1…r])这个函数的作用是将已经有序的a[p…q]和a[q+1…r]合并成一个有序数组，并且放入a[p…r]。那这个过程如何实现呢？

如下图所示，我们申请一个临时数组tmp，大小与a[p…r]相同。我们用两个游标i和j，分别指向a[p…q]和a[q+1…r]到第一个元素。比较这两个元素a[i]和a[j]，如果a[i]<=a[j]，我们就把a[i]放入到临时数组tmp，并且i后移一位，否则将a[j]放入到数组tmp，j后移一位。

重复上述比较过程，直到其中一个子数组中的所有数据都放入临时数组中，再把另一个数组中的数据依次加入到临时数组的末尾，这个时候，临时数组中存储的就是两个子数组合并之后的结果了。最后再把临时数组tmp中的数据拷贝到原始数组a[p…r]中。

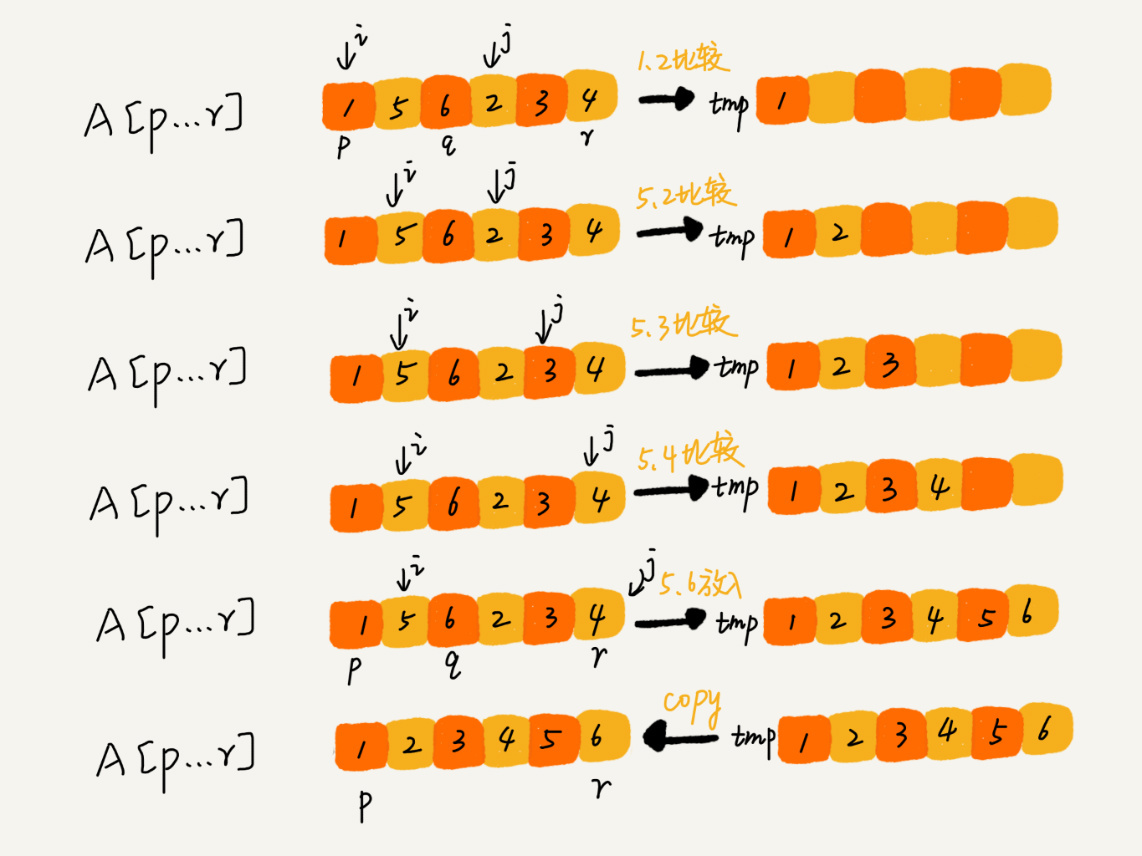
所以完善上面merge()函数的代码，就是下面这样

public void merge(int[] a, int p, int r, int q) {
  //初始化变量 i ，j，k
  int i = p;
  int j = q + 1;
  int k = 0;
  int[] tmp = new int[r-p+1]; //申请一个大小跟a[p...r]一样的临时数组
  while(i <= q && j <= r) {
    if (a[i] <= a[j]) {
      tmp[k++] = a[i++]; 
    } else {
      tmp[k++] = a[j++];
    }
  }

  //判断哪个子数组中有剩余的数据
  int start = i, end = q;
  if (j <= r) {
    start = j;
    end = r;
  }
  //将剩余的数据拷贝到临时数组tmp
  while (start <= end) {
    tmp[k++] = a[start++];
  }
  //将tmp中的数组拷贝回a[p...r]
  for (i = 0; i <= r - p; i++) {
    a[p+i] = tmp[i];
  }
}

上述代码可以利用哨兵机制进行边界处理，代码会简洁很多。

归并排序的性能分析

• 归并排序是稳定的排序算法吗？

  归并排序稳不稳定关键要看merge()函数，也就是两个有序子数组合并成一个有序数组的那部分代码。

  在合并的过程中，如果a[p…q]和a[q+1…r]之间有值相同的元素，那我们可以先把a[p…q]中的元素放入tmp数组。这样就保证了值相同的元素，在合并前后的先后顺序不变，所以，归并排序是一个稳定的排序算法。

• 归并排序的时间复杂度是多少？

  归并排序涉及递归，递归的适用场景是，一个问题a可以分解为多个子问题b、c，那求解问题a就可以分解为求解问题b、c。问题b、c解决之后，我们再把b、c的结果合并成a的结果。

  如果我们定义求解问题a的时间是T(a)，求解问题b、c的时间分别是T(b)和T(c)，那就可以得到这样的递推公式：

  T(a) = T(b) + T(c) + K
  

  其中K等于将两个子问题b、c的结果合并成问题a的结果所消耗的时间。

  由此得出一个重要的结论：不仅递归求解的问题可以写成递推公式，递归代码的时间复杂度也可以写成递推公式。

  我们假设对n个元素进行归并排序需要的时间是T(n)，那分解成两个子数组排序的时间都是T(n/2)。由于merge()函数合并两个有序子数组的时间复杂度是O(n)。所以套用前面的公式，归并排序的时间复杂度的计算公式为：

  T(1) = C；   n=1 时，只需要常量级的执行时间，所以表示为 C。
  T(n) = 2*T(n/2) + n； n>1
  

  通过这个公式，再进一步分解求解的计算过程。

  T(n) = 2*T(n/2) + n
       = 2*(2*T(n/4) + n/2) + n = 4*T(n/4) + 2*n
       = 4*(2*T(n/8) + n/4) + 2*n = 8*T(n/8) + 3*n
       = 8*(2*T(n/16) + n/8) + 3*n = 16*T(n/16) + 4*n
       ......
       = 2ᵏ * T(n/2ᵏ) + k * n
       ......
  

  所以我们可以得到T(n) = 2ᵏT(n/2ᵏ)+kn。当T(n/2ᵏ)=T(1)时，也就是n/2ᵏ=1，我们得到k=㏒₂n。我们将k值代入上面的公式，得到T(n)=Cn+n㏒₂n。用大O标记法来表示的话，T(n)就等于O(n㏒n)。所以归并排序的时间复杂度是O(n㏒n)。

  通过归并排序的原理和代码可以看出，归并排序的执行效率与要排序的原始数组的有序程度无关，所以其时间复杂度是非常稳定的，不管是最好情况、最坏情况，还是平均情况，时间复杂度都是O(n㏒n)。

• 归并排序的空间复杂度是多少？

  虽然归并排序的时间复杂度在任何情况下都是O(n㏒n)，但是归并排序并没有像快排那样应用广泛，因为归并排序有一个致命的“弱点”，那就是归并排序不是原地排序算法。

  这是因为归并排序的合并函数，在合并两个有序数组为一个有序数组时，需要借助额外的存储空间。那归并排序的空间复杂度到底是多少呢？该如何分析？

  如果我们继续按照分析递归时间复杂度的方法，通过递推公式来求解，那整个归并过程需要的空间复杂度就是O(n㏒n)。不过这个分析思路是有问题的。

  实际上，递归代码的空间复杂度并不能像时间复杂度那样累加。尽管每次合并操作都需要申请额外的内存空间，但在合并完成之后，临时开辟的内存空间就被释放掉了。在任意时刻，CPU只会有一个函数在执行，也就只会有一个临时的内存空间在使用。临时内存空间最大也不会超过n个数据的大小，所以空间复杂度是O(n)。

快速排序的原理

快速排序(QuickSort)简称“快排”。快排利用的也是分治思想。它有点像归并排序，但是思路完全不一样。

快排的思想是这样的：如果要排序数组中下标从p到r之间的一组数据，我们选择p到r之间的任意一个数据作为pivot(分区点)。

我们遍历p到r之间的数据，将小于pivot的放左边，将大于pivot的放右边，将pivot放到中间。经过这一步骤之后，数组p到r之间的数据就被分成了三个部分，前面p到q-1之间都是小于pivot的，中间是pivot，后面的q+1到r之间是大于pivot的。

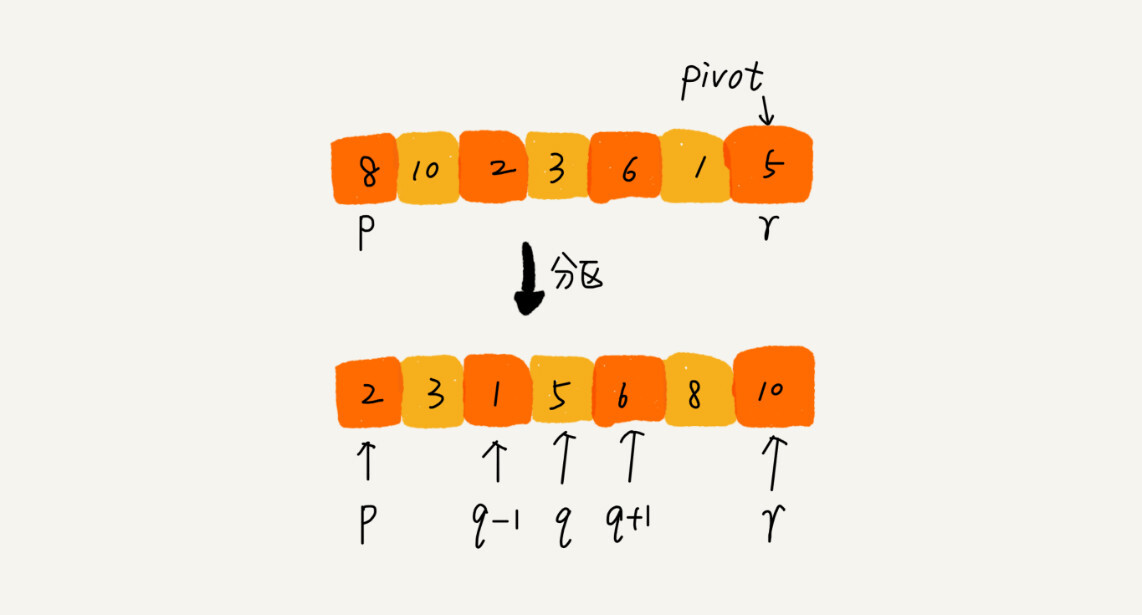
根据分治、递归的处理思想，我们可以用递归排序下标从p到q-1之间的数据和下标从q+1到r之间的数据，直到区间缩小为1，就说明所有的数据都有序了。

所以它的递推公式如下：

递推公式：
quick_sort(p…r) = quick_sort(p…q-1) + quick_sort(q+1… r)

终止条件：
p >= r

将递归公式翻译成递归代码如下：

//快速排序 ， a是数组， n表示数组的大小
public void quickSort(int[] a, int n) {
  quickSortC(a, 0, n-1);
}
//快速排序递归函数，p，r为下标
public void quickSortC(int[] a, int p, int r) {
  if (p >= r) return;
  
  int q = partition(a, p, r); //获取分区点
  quickSortC(a, p, q-1);
  quickSortC(a, q+1, r);
}

归并排序中有一个merge()合并函数，这里有一个partition()分区函数。partition()分区函数就是随机选择一个元素作为pivot(一般情况下，可以选择p到r区间的最后一个元素)，然后对a[p…r]分区，函数返回pivot的下标。

如果不考虑空间消耗的话，partition()分区函数可以写得非常简单。我们申请两个临时数组X和Y，遍历a[p….r]，将小于pivot的元素都拷贝到临时数组X，将大于pivot的元素都拷贝到临时数组Y，最后再将数组X和数组Y中数据顺序拷贝到a[p…r]。

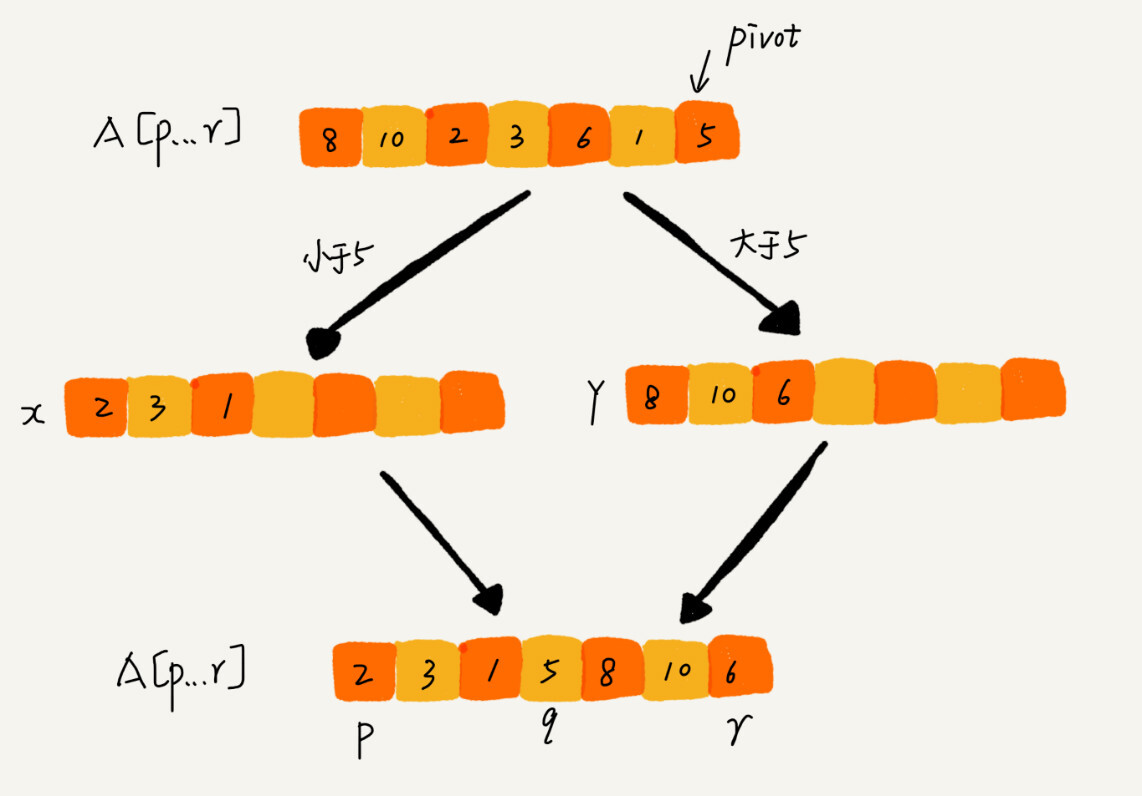
但是，照这种思路实现的话，partition()函数就需要很多额外的内存空间，所以快排就不是原地排序算法了。要想快排是原地排序算法，那它的空间复杂度必须是O(1)，那partition()分区函数就不能占用太多额外的内存空间，我们需要在a[p…r]的原地完成分区操作。

原地分区函数的实现思路非常巧妙，代码如下：

public int partition(int[] a, int p, int r) {
  int pivot = a[r];
  int i = p;
  int temp = 0;
  for (int j = p; j <= r-1; j++) {
    if (a[j] < pivot) {
      temp = a[i];
      a[i] = a[j];
      a[j] = temp;
      i++;
    }
  }
  temp = a[i];
  a[i] = a[r];
  a[r] = temp;
  return i;
}

这个处理有点类似选择排序。我们通过游标i把a[p…r-1]分成两部分。a[p…i-1]的元素都是小于pivot的，我们暂且叫它“已处理区间”，a[i…r-1]是“未处理区间”。我们每次都从未处理的区间a[i…r-1]中取一个元素a[j]，与pivot对比，如果小于pivot，则将其加入到已处理区间的尾部，也就是a[i]的位置。

在数组某个位置插入元素，需要搬移数据，非常耗时。我们可以通过交换，在O(1)的时间复杂度内完成插入操作。这里我们也借助这个思想，只需要将a[i]和a[j]交换，就可以在O(1)时间复杂度内将a[j]放到下标为i的位置。

用图来展示分区的整个过程如下：

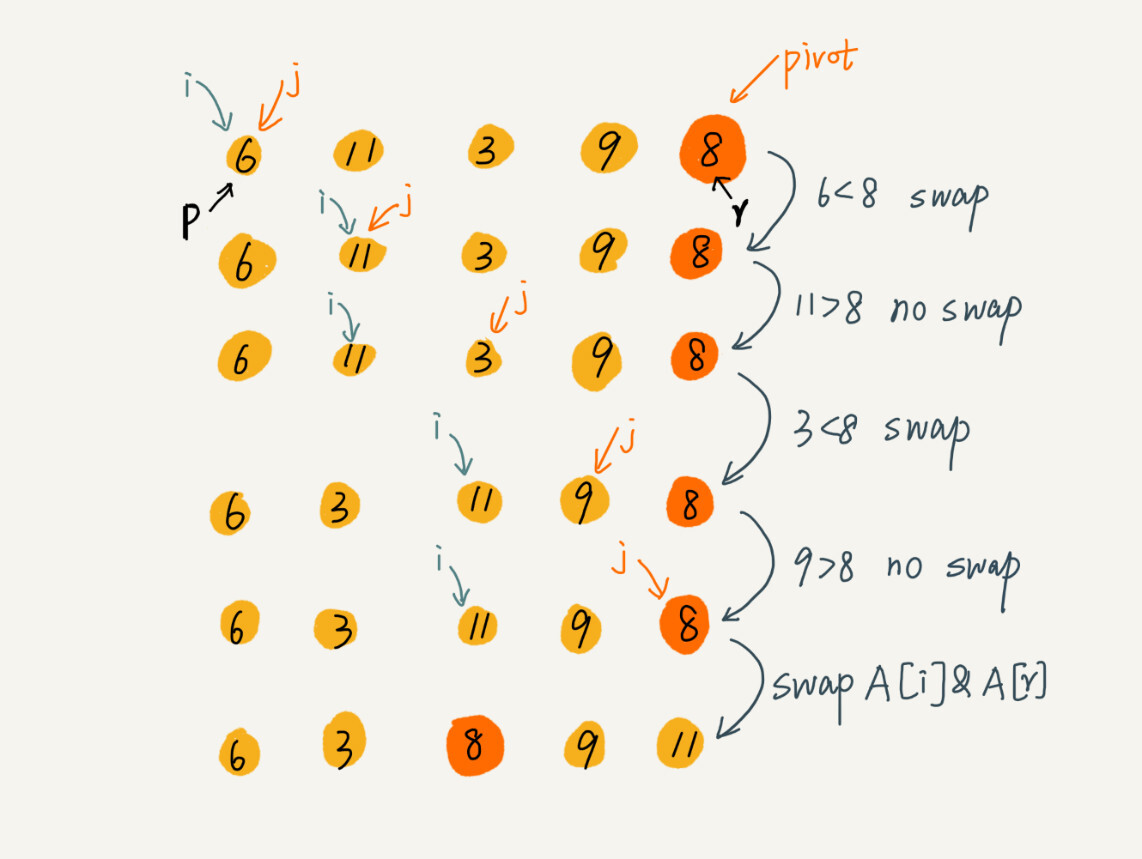
因为分区的过程涉及交换操作，如果数组中有两个相同的元素，比如序列6，8，7，6，3，5，9，4，在经过第一次分区操作之后，两个6的相对先后顺序就会改变。所以，快速排序并不是一个稳定的排序算法。

快排和归并用的都是分治思想，递推公式和递归代码也非常相似，那它们之间的区别是什么呢？

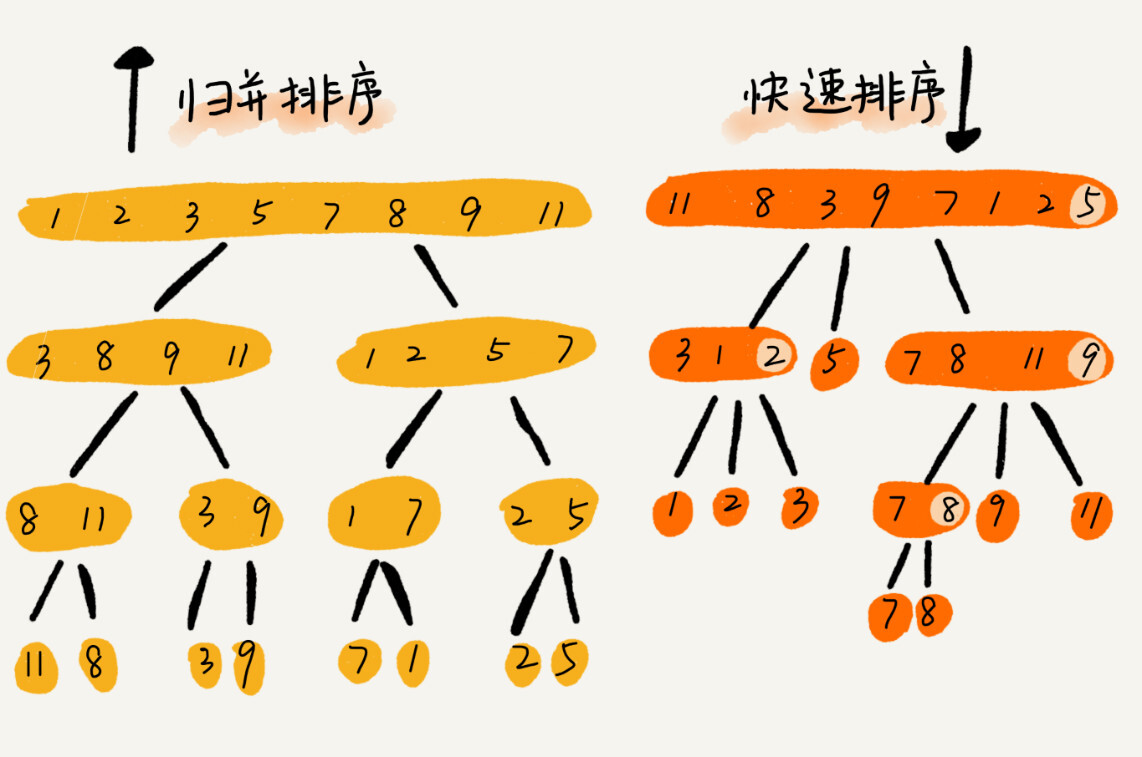
归并排序的处理过程是由下到上的，先处理子问题，然后再合并。而快排正好相反，它的处理过程是由上到下的，先分区，然后再处理子问题。归并排序虽然是稳定的、时间复杂度为O(n㏒n)的排序算法，但是它是非原地排序算法，因为归并排序的合并函数无法在原地执行。快速排序通过设计巧妙的原地分区函数，可以实现原地排序，解决了归并排序占用太多内存的问题。

快速排序的性能分析

快排是一种原地、不稳定的排序算法，那它的时间复杂度是多少呢？

快排也是用递归来实现的。如果每次分区操作，都能正好把数组分成大小接近相等的两个区间，那快排的时间复杂度递推求解公式跟归并是相同的。所以，快排的时间复杂度也是O(n㏒n)。

T(1) = C；   n=1 时，只需要常量级的执行时间，所以表示为 C。
T(n) = 2*T(n/2) + n； n>1

但是，公式成立的前提是每次分区操作，我们选择的pivot都正合适，正好能将大区间对等地一分为二。但实际上这种情况是很难实现的。

比如：如果数组中的数据原来已经是有序的了，例如1，3，5，6，8。如果每次选择最后一个元素作为pivot，那每次分区得到的两个区间都是不均等的。我们需要进行大约n次这样的分区操作，才能完成快排的整个过程。每次分区我们平均要扫描大约n/2个元素，这种情况下，快排的时间复杂度就从O(n㏒n)退化成了O(n²)。

以上都是两个极端情况下的时间复杂度，一个是分区及其均衡，一个是分区及其不均衡。他们分别对应快排的最好情况时间复杂度和最坏情况时间复杂度。那快排的平均情况时间复杂度是多少呢？

假设每次分区操作都将区间分成大小为9:1的两个小区间。我们继续套用递归时间复杂度的递推公式，就会变成这样：

T(1) = C；   n=1 时，只需要常量级的执行时间，所以表示为 C。
T(n) = T(n/10) + T(9*n/10) + n； n>1

这个递推公式求解过程非常复杂，不推荐用这种方法。递归的时间复杂度的求解方法除了递推公式之外，还有递归树。这里直接给出结论：T(n)在大部分情况下的时间复杂度都可以做到O(n㏒n)，只有在极端情况下，才会退化到O(n²)。而且，有很多方法可以将这个极端概率降到很低，如何来做？后面再说。

解答开篇

快排核心思想就是分治和分区。利用分区思想，可以解答开篇问题：O(n)时间复杂度内求无序数组中的第K大元素。比如，4，2，5，12，3这样一组数据，第3大元素就是4。

我们选择数组区间a[0…n-1]的最后一个元素a[n-1]作为pivot，对数组a[0…n-1]原地分区，这样数组就分成了三部分，a[0….p-1]、a[p]、a[p+1….n-1]。

如果p+1=K，那a[p]就是要求解的元素；如果K>p+1，说明第K大元素出现在a[p+1….n-1]区间，我们再按照上面的思路递归地在a[p+1….n-1]这个区间内查找。同理，如果K<p+1，那我们就在a[0…p-1]区间查找。

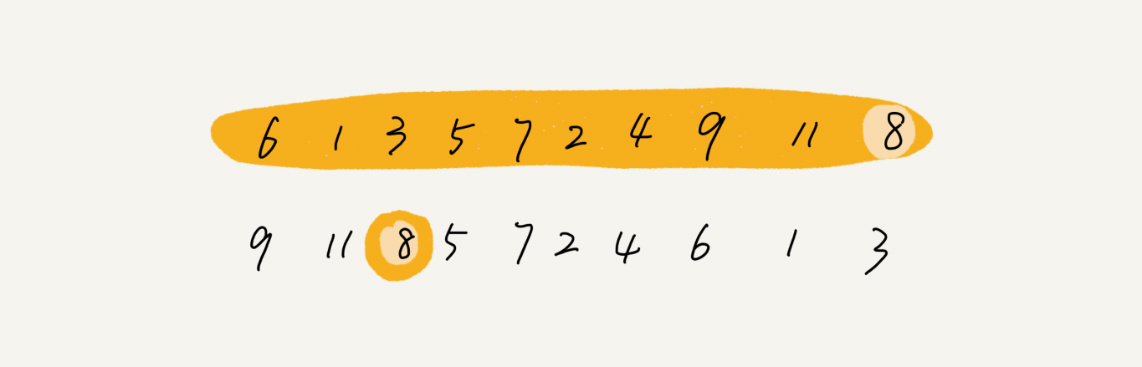
对应的代码如下：

public static int findKthLargest(int[] nums, int k) {
	return quickSort(nums, 0, nums.length-1, k);
}
	
public static int quickSort(int[] nums, int s, int e, int k) {
  int pivot = nums[e];
  int i = s;
  int temp = 0;

  for (int j = s; j <= e - 1; j++) {
    if (nums[j] > pivot) {
      temp = nums[j];
      nums[j] = nums[i];
      nums[i] = temp;
      i++;
    }
  }
  temp = nums[e];
  nums[e] = nums[i];
  nums[i] = temp;

  if (i + 1 == k) {
    return nums[i];
  } else if (i + 1 < k) {
    return quickSort(nums, i+1, e, k);
  } else {
    return quickSort(nums, s, i-1, k);
  }
}

为什么上述解决思路的时间复杂度是O(n)？

第一次分区查找，我们需要对大小为n的数组执行分区操作，需要遍历n个元素。第二次分区查找，我们只需要对大小为n/2的数组执行分区操作，需要遍历n/2个元素。依此类推，分区遍历元素的个数分别为n、n/2、n/4、n/8、n/16….直到区间缩小为1。

如果我们把每次分区遍历的元素个数加起来，就是n+n/2+n/4+n/8+….1。这是一个等比数列求和，最后的和等于2n-1。所以，上述解决思路的时间复杂度就是O(n)。

当然你可以用暴力求解的思路：每次取数组中的最大值，将其移动到数组的最前面，然后在剩下的数组中继续找最大值，以此类推，执行K次，找到的数据就是第K大元素。

但是这个暴力求解的时间复杂度并不是O(n)，而是O(k*n)。这里的系数K是比较小的常量时，比如1、2，那最好时间复杂度确实是O(n)，但当K=n/2或者等于n时，这种最坏情况下的时间复杂度就是O(n²)了。

小结

归并排序和快速排序是两种稍微复杂的排序算法，它们用的都是分治的思想，代码都通过递归来实现，过程非常相似。理解归并排序的重点是理解递推公式和merge()合并函数。理解快速排序的重点也是理解递推公式，还有partition()分区函数。

归并排序算法是一种在任何情况下时间复杂度都比较稳定的排序算法，这也使它存在的致命的缺点，即归并排序不是原地排序算法，空间复杂度比较高，为O(n)。因此，它没有快排应用广泛。

快速排序算法虽然最坏情况下的时间复杂度是O(n²)，但是平均情况下的时间复杂度都是O(n㏒n)。不仅如此，快速排序算法时间复杂度退化到O(n²)的概率非常小，我们可以通过合理地选择pivot来避免这种情况。

思考

现在有10个接口访问日志文件，每个日志文件大小约300MB，每个文件里的日志都是按照时间戳从小到大排序的。要想将这10个较小的日志文件，合并为1个日志文件，合并之后的日志仍然按照时间戳从小到大排序。如果处理上述排序任务的机器内存只有1GB，有什么思路能“快速”地将这10个日志文件合并？¹